The Los Alamos Primer

• 15 February 2025
• physics

Part 1

I recently watched a lecture on how nuclear weapons are designed. It mentioned a few reading recommendations for anyone wanting to learn more, and one of those was The Los Alamos Primer. The primer itself is interesting for several reasons: it’s pretty old—mid-1940s old—and it’s based on five lectures Robert Serber gave in early 1943. If you open it up, you’ll see it’s very direct and technical, jumping right into things from the very first paragraph:

The object of the project is to produce a practical military weapon in the form of a bomb in which the energy is released by a fast neutron chain reaction in one or more of the materials known to show nuclear fission. It was classified for a long time but is now available publicly. Due to its historical and academic context I was sure I wanted to read it.

I should mention something if you plan to buy it, though: I don’t recommend getting the paperback edition with that portrait on the cover (possibly of R. Serber?). I ordered one off Amazon, and it turned out to be the public-domain PDF hastily printed on flimsy paper. You might actually find it easier to read directly from the online PDF instead. But I digress.

Why This Write-Up?

My goal here is twofold: it helps me cement my own understanding by writing about it, and it might help anyone else trying to parse The Los Alamos Primer. The text skips some steps, uses older notation, and can be quite dense. Filling in the gaps and clarifying terminology felt like a good idea.

Units

One thing to note: The Primer uses the centimeter–gram–second (CGS) system instead of SI units. The differences aren’t huge in most places—centimeters instead of meters, ergs instead of joules—but it’s worth keeping in mind if you’re more comfortable with SI.

Terminology

You also won’t see actual element names in the text. Uranium-235 is just called “25,” and Uranium-238 is “28.” Plutonium (with atomic number 94) is referred to as “49.” At the time, they might not have even settled on the name “plutonium.” It’s all very cloak-and-dagger.

Energy of the Fission Process

The Primer starts with some back-of-the-envelope calculations about energy released from fission. It assumes an energy of about $200\mathrm{MeV}$ per atom. One quick calculation shown is: $$170\times {10}^6\times 4.8\times {10}^{-10}/300=2.7\times {10}^{-4}\text{erg/nucleus}$$

Two things to point out:

• $4.8\times {10}^{-10}$ is a conversion factor from MeV to ergs
• I'm not sure I understand where the factor of $1/300$ is coming from (could it be trying to account for the number of nuclei per atom?)

We then take the weight of one nucleus to be $3.88\times {10}^{-22}$ and arrive at a final figure of $7\times {10}^{17}$ ergs per gram. According to the primer this means that fissioning 1kg of uranium 235 would yield the equivalent of 20000 tons of TNT.

Fast Neutron Chain Reaction

Things pick up fast here. The Primer notes that since each fission event—triggered by a neutron—releases about two neutrons, you can get an exponential increase in neutron count. It makes two very idealized assumptions for the sake of simplicity:

1. No neutrons escape through the surface.
2. The material is perfectly pure, so no neutrons are wasted in other reactions.

Under those assumptions, the Primer figures you’d need around 80 “generations” of neutrons to fission a kilogram of U-235. Of course, in reality, you do lose neutrons through the surface, and not all are used purely for fission. The rest of the Primer goes deep into how to handle that.

For one, we'll have some neutrons diffuse out through the surface of the material. If we assume that we have our fissile material fashioned into a sphere than we can consider that it has some given surface losses of neutrons through the surface. There will be a point where these surface losses will be enough to stop our chain reaction. Just as the rate of the internal neutron generation depends on the material density, so does our surface loss component. The question now is how the relationship between those two terms changes as the sphere expands under the pressure and temperature build-up.

If the minimum radius required for the chain reaction to stop grows faster than the actual sphere expansion we can sustain an explosive chain reaction. Otherwise we cannot have an effective explosion. This hints at why the fission process needs to happen extremely fast—before the bomb blows itself apart and halts the chain reaction.

Another interesting note: each nucleus releases so much energy that even if only 0.5% of the available energy is released, the material’s temperature skyrockets to about ${10}^7$ degrees, leading to intense ionization. If 1% is released, the average speed of the nuclear particles can be around ${10}^8$ cm/s.

Let's step through how to arrive at these estimates.

Temperature

We take the $170\text{MeV}$ of fission energy per atom. A heavy nucleus (such as Uranium, Plutonium, etc.) has roughly 200 nucleons (protons+neutrons). As a rough order of magnitude we can assume $A=200$. Let's take the 0.5% case first. We have $$\frac{E_{fis}}{A}=\frac{170\text{MeV}\times 0.005}{200}=4.25\text{keV}$$ Taking $k_{B}T=E$ and rearranging we get $$T=\frac{E}{k_B}=\frac{4.25\times {10}^3}{8.617\times {10}^{-5}}\approx 49\times {10}^{6}K$$ which is on the same order of magnitude as what the primer lists.

Mean speed

Given we have double the energy available (i.e. 1% vs 0.5% from the last example) we have 8.5 keV per nucleon. Taking the mass of one to be $1.67\times {10}^{-27}\text{kg}$ and plugging into $$\frac{1}{2}m{v}^2=E$$ and rearranging $$v=\sqrt{\frac{2E}{m}}=\sqrt{\frac{2\times 8.5\times {10}^3\times \alpha }{1.67\times {10}^{-27}}}=1.27\times {10}^8\text{cm/s}$$ where $\alpha =1.6\times {10}^{-19}$ is a conversion factor from keV to Joules.

There are two key points to take in from this.

1. Given the speeds we're dealing with we need the whole fission reaction to occur very quickly. Assuming an expansion of 5cm is enough to stop the criticality we need the process completed in $5\times {10}^{-8}$ seconds.
2. Slow neutrons are useless to us exactly because of the point above.

Fission Cross-sections

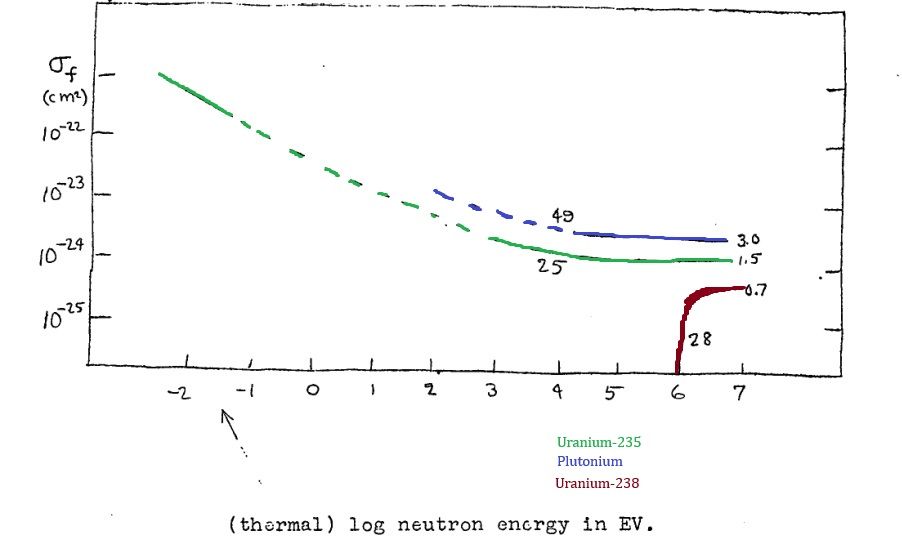
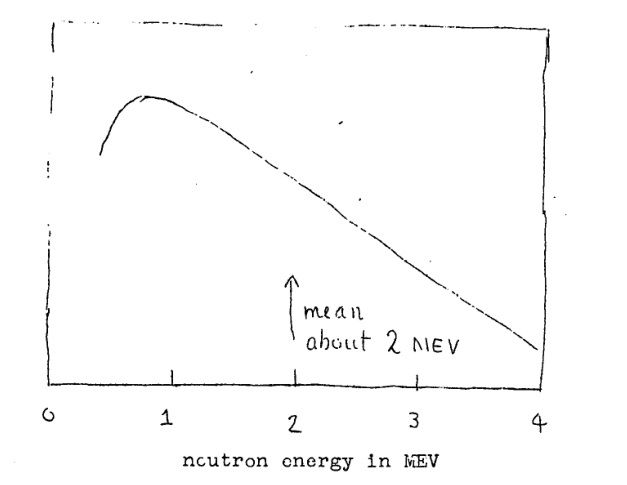
The Primer includes a plot of fission cross-sections for U-235, U-238, and plutonium. The key takeaway is that U-238 (which is 99.3% of natural uranium) only has a significant cross-section above about 1 MeV. Another graph shows the energy distribution of neutrons released in fission. Most fission neutrons do have energies around 1 MeV or higher, but not all stay that energetic for long.

Neutron number

The neutron number $\nu$ is simply the average number of neutrons produced per fission reaction. For the purpose of inducing a self-supporting fission reaction we will need $\nu >1$.

Why ordinary uranium is safe

Since U-238 makes up about 99.3% of natural uranium, the Primer points out two reasons it can’t sustain a fast chain reaction:

1. Only about 3/4 of generated neutrons will be above 1 MeV.
2. About 1/4 of those neutrons are lost before they can cause fission.

Starting with an initial neutron number of $2.2$ and factoring in the above we get an effective neutron number of: $$\nu =2.2\times 3/4\times 1/4=0.4$$ Starting with an initial neutron number of around 2, then factoring in those losses, you drop below 1, which kills the chain reaction. U-235 can save the day, but it’s only about 0.7% of natural uranium, so you need to enrich it first.

Note

I'm happy to accept the 3/4 factor: it seems sensible enough given the neutron energy distribution and the cross section plot referenced earlier. I'm sure we'll have far more accurate data on both now but we're trying to work off what was available at the time.

I've tried to run simple simulations to work out where the 1/4 factor is coming from but I was getting wildly different results. I.e. I wanted to work out the chances of a neutron causing a fission reaction BEFORE it's slowed down below ~1MeV level. This means factoring in inelastic and elastic collisions with their respective probabilities. However, I think there might be a few key factors missing from my attempts:

• The cross-sections are energy dependent
  • The inelastic cross-sections vary with energy and have thresholds
  • Even elastic scattering changes with energy
• The geometry matters too
  • The actual path length through the material
  • The probability of leaving the material entirely
  • The effects of spatial distribution
• The end probability of being slowed down will depend heavily on the starting energy as well

In the end I'm not sure where the 1/4 factor is coming from. It's likely a very conservative estimate based on limited experimental data available at the time and some simplified calculations that could be done without computers.

Making plutonium

Section 10 of the primer talks about "element 49" which we now know as plutonium. At the time the notes were written only minute amounts had been created though. The section ends with:

since there is every reason to expect its $\nu$ to be close to that for [uranium] and since it is fissionable with slow neutrons it is expected to be suitable for our problem and anothor project is going forward with plans to produce it for us in kilogram quantities. Further study of all its properties has an important place on our program as rapidly as suiteable quantities become available.

Spoiler alert: they did end up producing large quantites of it, and they did use it in Fat Man.

TBC

I’ll stop here for now. In my next post, I’ll get into the Primer’s discussion on minimum bomb sizes, tamper effects, and their early rough estimates of damage and shockwave behavior.